1 A l’origine, la lumière…

1.1 Le rayonnement électromagnétique

La lumière est un rayonnement électromagnétique qui peut être modélisé par une onde électromagnétique (comportement ondulatoire) ou un ensemble de photons (comportement corpusculaire). Dans le premier cas, l’onde électromagnétique se décompose en un champ électrique et un champ magnétique. D’après la théorie ondulatoire de la lumière, tout rayonnement peut alors être considéré comme la superposition d’ondes planes monochromatiques caractérisées par leurs longueurs d’onde et leurs fréquences. La notion d’onde électromagnétique est complémentaire de celle du photon, une particule sans masse et sans charge électrique, qui est associé à une radiation électromagnétique monochromatique.

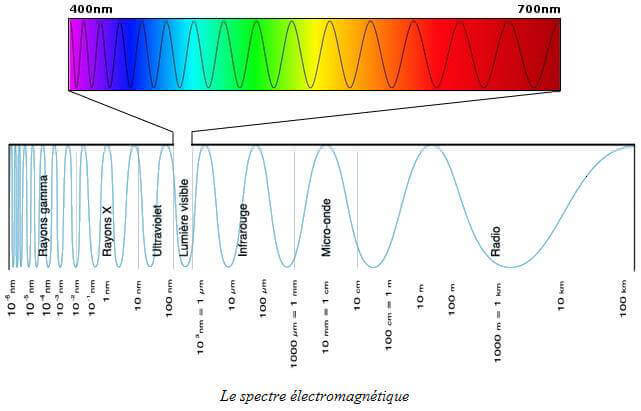
Le spectre électromagnétique est la décomposition du rayonnement électromagnétique selon ses différentes composantes en termes de fréquence ([latex]\nu[/latex]), de longueur d’onde ([latex]\lambda[/latex]) et d’énergie des photons (E). La figure 1 montre une représentation de ce spectre en fonction de la longueur d’onde. Les trois grandeurs sont liées deux à deux par la constante de Planck ([latex]h=6.62617.10^{-34}J.s[/latex]) et la vitesse de la lumière dans le vide ([latex]c=299792458 m.s^{-1}[/latex]) :

[latex]E=\left[hc\right]/{\lambda}[/latex]

La gamme de longueurs d’onde qui nous intéresse s’étend du visible (0.30 à 1.30 µm) au proche infrarouge (1.30 µm à 2.50 µm). En terme de fréquence, elle se situe autour de [latex]10^{8}MHz[/latex] et est donc difficile à mesurer par les instruments actuels. Pour quantifier le rayonnement électromagnétique sur cette gamme de longueurs d’onde, il est plus aisé de se servir de la quantité de photons reçus. Les capteurs utilisés en spectroscopie sont donc basés sur ce principe. L’équation nous montre qu’il est possible de relier cette quantité de photon à une longueur d’onde donnée. La longueur d’onde sera une unité de référence dans la suite de ce travail et sera exprimée en nanomètres (nm) ou micromètres (µm).

1.2 Source lumineuse

La source d’un rayonnement électromagnétique est l’agitation thermique des particules : les matériaux émettent un rayonnement caractéristique qui est fonction de leurs températures. Un corps noir est un émetteur thermique idéal qui absorbe tout ce qu’il reçoit et réémet à toutes les longueurs d’onde. La luminance du corps noir à une longueur d’onde donnée est définie selon la loi de Planck :

[latex]L_{\lambda}=\left[{2hc^{2}\lambda^{-5}}\right]/{\left[{exp(\frac{hc}{kT\lambda})-1}\right]}[/latex]

avec k la constante de Boltzmann ([latex]k = 1,38066.10^{-23}[/latex]) et T la température en Kelvin. Les courbes d’émission d’un corps noir à différentes températures sont données dans la figure 2. La principale source lumineuse émettrice de photons est pour nous le Soleil qui est considéré comme ayant le comportement d’un corps noir.

L’émissivité d’un matériau ([latex]\varepsilon[/latex]) est alors le rapport entre l’énergie qu’il rayonne et celle à laquelle rayonnerait un corps noir à la même température. L’émissivité dépend donc aussi de la température et de la longueur d’onde. A l’inverse du visible et du proche-infrarouge, l’infrarouge thermique (au delà de 2.50 µm) correspond au domaine de longueur d’onde pour lequel le rayonnement propre du corps est mesuré.

2 Notions de photométrie : les principales grandeurs

2.1 Angles d’incidence, d’émergence et de phase et angle solide

Les photons émis par la source vont interagir avec la matière en un point. L’observation consiste à analyser le signal résultant de cette interaction. Les trois paramètres qui sont utilisés pour caractériser une observation sont tout d’abord l’angle d’incidence (i) défini comme l’angle entre la source lumineuse et la normale à la surface au point où les photons interagissent. Ensuite, le deuxième paramètre est l’angle d’émergence (e) qui correspond à l’angle entre la normale à la surface et la position de l’observateur. Enfin, l’angle de phase [latex](\varphi)[/latex] est l’angle entre la source lumineuse et l’observateur. Ces trois paramètres sont représentés sur la figure 3.

Pour calculer l’angle solide ([latex]\Omega[/latex]) sous lequel un objet peut être vu en un point donné, l’objet est projeté sur une sphère de rayon r (exemple pour un objet sphérique sur la figure 4). L’angle solide, exprimé en stéradians (Sr), correspond alors au rapport entre la surface que forme la projection de l’objet et le carré du rayon de cette sphère ([latex]\Omega={S}/{r^{2}}[/latex]).

2.2 Luminance

Le terme puissance (en Watts), ou flux rayonné ([latex]F_{r}[/latex] en [latex]J.s^{-1}[/latex]), désigne la quantité d’énergie qui est émise ou reçue par un corps par unité de temps, et ce dans toutes les directions. L’émittance (M en [latex]W.m^{-2}[/latex]) est la puissance émise par unité de surface d’une source étendue dans tout un hémisphère. Pour les surfaces, par opposition aux sources, la puissance reçue par unité de surface dans tout un hémisphère est appelé éclairement (E).

La luminance (L en [latex]W.m^{-2}.sr^{-1}[/latex]) est quant à elle la puissance émise par une source dans une direction donnée en fonction de l’angle solide et de la surface apparente. L’énergie mesurée au niveau d’un capteur est donc proportionnelle à la luminance de la source observée.

[latex]L=\frac{dF_{r}}{dS.d\Omega.\cos\theta}[/latex]

où [latex]\theta[/latex] est l’angle entre l’élément de surface dS et la source. On parle de luminance spectrale quand la longueur d’onde est prise en compte ([latex]\frac{dL}{d\lambda}[/latex]). Pour un corps noir et à une longueur d’onde donnée, la luminance est uniquement fonction de la température.

2.3 Réflectance

La réflectance diffuse, ou réflectance directionnelle hémisphérique, est la fraction du flux réémis dans toutes les directions à la longueur d’onde [latex]\lambda[/latex] pour un éclairage collimaté sous incidence i. La réflectance bidirectionnelle est alors la fraction du flux réémis par une surface en direction de l’observateur pour un éclairage collimaté. En plus de i et [latex]\lambda[/latex], elle dépend donc aussi de l’angle d’émergence et de la phase. Elle est alors notée r(i,e,[latex]\varphi[/latex],[latex]\lambda[/latex]) et s’exprime en [latex]Sr^{-1}[/latex].

[latex]r(i,e,\varphi,\lambda)=\frac{L_{e}}{E_{i}}=\frac{I}{\pi F}[/latex]

A partir de la réflectance bidirectionnelle, il est possible de définir trois grandeurs supplémentaires que sont le facteur de radiance (RADF, RADiance Factor), la fonction de distribution de r (Bidirectional Reflectance Distribution Fonction, BRDF, aussi noté [latex]\rho[/latex]) et le facteur de réflectance (REFF, REFlectance Factor).

3 Mesure par un capteur

3.1 Principe de fonctionnement

La fonction du capteur est d’analyser le signal émis par une surface planétaire et ce à différentes longueurs d’onde. Comme cela a été expliqué précédemment, le flux de photons est le plus facile à analyser. Un système optique collecte donc le rayonnement réfléchi par la surface et l’envoie sur un dispositif de sélection de longueur d’onde (e.g. un prisme ). Le détecteur enregistre ensuite, pour chaque longueur d’onde, le nombre de photons ayant frappé sa surface. Dans le cas de l’imagerie hyperspectrale, la dimension spatiale se rajoute à la dimension spectrale. Les capteurs qui sont couramment utilisés sont de type CCD (Charged Coupled Device). Ils se présentent sous la forme de matrice ou de barrette et sont formés d’un ensemble de détecteurs indépendants (pixel) qui analyseront chacun une petite portion de la surface observée.

Pour passer du signal reçu par l’instrument à la réflectance (ou à l’émissivité) de la surface, il faut à la fois tenir compte des paramètres physiques décrits précédemment et des paramètres instrumentaux. Une fonction de transfert, calibrée à la fois au sol et pendant le vol, est utilisée et permet de faire la conversion. Sont ainsi pris en compte le ” dark ”, c’est-à-dire le signal résiduel dû à l’agitation thermique (ou courant d’obscurité), et le ” flat ” qui décrit les variations de réponse du détecteur sous un éclairage uniforme.

3.2 Grandeur mesurée par un capteur

Dans le cas d’une surface naturelle rugueuse, la lumière est réémise de manière non isotrope. Si la source lumineuse est le Soleil, alors la luminance correspondant au flux solaire réfléchi par la surface dans une direction donnée est :

[latex]\frac{dL}{d\lambda}=\rho(i,e,\varphi,\lambda)\frac{\pi R_{Soleil}^{2}\lambda}{D_{Soleil}^{2}}B_{\lambda}T_{Soleil}\cos i[/latex]

avec [latex]R_{Soleil}[/latex], [latex]D_{Soleil}[/latex], et [latex]B_{\lambda}T_{Soleil}[/latex] respectivement le rayon du Soleil, la distance entre le Soleil et la surface et la luminance spectrale du Soleil. La luminance spectrale d’un corps noir s’exprime suivant la relation

[latex]B_{\lambda}T=\frac{2hc^{2}\lambda^{-5}}{e^{hc/kT\lambda}-1}[/latex]

en [latex]W.m^{-2}.Sr^{-1}.{\mu}m^{-1}[/latex] avec h la constante de Planck, c la vitesse de la lumière, k la constante de Boltzmann et T la température en Kelvin.

Toutefois, en plus de la lumière émise par la source lumineuse, la surface contribue également au signal . En effet, celle-ci possède une température propre et émet donc un rayonnement. La contribution de la surface vient se rajouter à l’équation et le flux total vu par le détecteur devient :

[latex]\frac{dL}{d\lambda}=\rho(i,e,\varphi,\lambda)\left[\frac{{\pi}R_{Soleil}^{2}\lambda}{D_{Soleil}^{2}}\right]B_{\lambda}T_{Soleil}\cos{i}+\varepsilon_{\lambda}B_{\lambda}T_{Surface}[/latex]

Dans le cas de surfaces planétaires, la gamme de température implique une émissivité importante au delà de 3-4 µm : on parlera alors d’infrarouge thermique.